在时尚的璀璨舞台上,总有一些面孔,如同初绽的花朵,带着清新与灵动,让人眼前一亮。今天,我要向大家介绍的,就是这样一位拥有清纯气质与无限潜力的模特新星——杨丽洁,艺名:冰糖。

冰糖出生于2001年6月4日,来自四川这片充满活力与热情的土地。她有着一张清纯可爱的容颜,仿佛是大自然精心雕琢的艺术品。她那双大眼睛,如同璀璨的星辰,闪烁着对世界的好奇与热爱。每一次凝视她的眼睛,都能感受到一种心灵的纯净之美,仿佛能透过她的眼眸,看到最真挚的情感与最美好的憧憬。
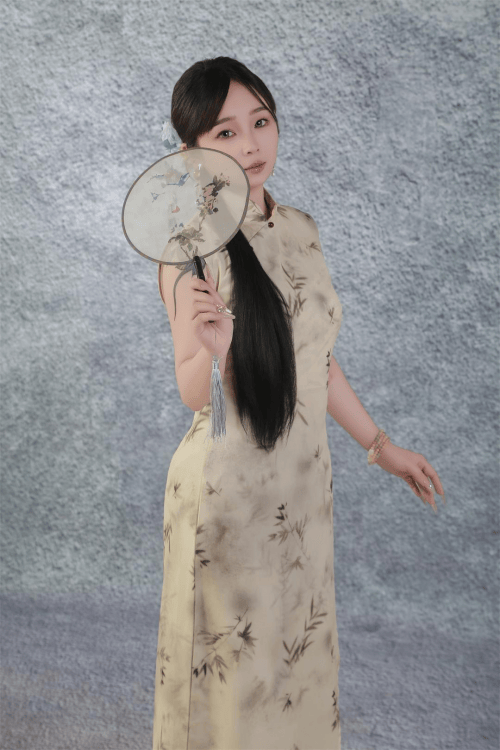
冰糖的气质清雅绝俗,宛如朝露初凝,带着一份纯真无邪,令人心生向往。她的肌肤胜雪,细腻光滑,仿佛能映照出世间最纯净的光芒。而她那清澈的眼眸,似含春水,顾盼生姿,一举一动间都散发着一种清雅高华的气质,让人不禁为之倾倒。她的笑容,更是如同春日暖阳,温暖而明媚,一颦一笑皆令人心醉不已。在她的身上,你能看到青春的活力与灵动,也能感受到一种独特的韵味,仿佛是大自然赋予她的独特魅力。

作为一名自由职业者,冰糖对于模特和演员的发展有着强烈的渴望与追求。她的身高虽然只有155厘米,但她的灵动与可爱,却让她在镜头前展现出独特的魅力。她的体重48公斤,身材娇小玲珑,却有着强大的气场与表现力。她的特长是唱歌,那清脆动听的嗓音,如同天籁之音,为她的舞台表演增添了一份独特的魅力。而她对吃喝玩乐的爱好,也让她拥有了对生活的热爱与热情,这种热爱与热情也体现在她的每一次表演中,让她在舞台上更加自信与从容。

冰糖喜欢的『明星』️是『邓紫棋』,她从『邓紫棋』身上汲取力量与灵感,学习她的坚韧与勇敢,努力在自己的道路上不断前行。虽然目前她还没有太多代表作品,但她的每一次尝试与努力,都让我们看到了她的潜力与未来。她参与过广告拍摄,虽然经验尚浅,但每一次的拍摄,她都全力以赴,展现出自己最好的一面。她的外形风格清新自然,带着一种独特的时尚感,无论是甜美可爱的风格,还是清新文艺的风格,她都能轻松驾驭,展现出自己独特的魅力。
在才艺表演学习经历方面,冰糖也从未停止过努力。她通过各种渠道学习表演技巧,提升自己的专业素养。她深知,作为一名模特和演员,只有不断提升自己,才能在竞争激烈的行业中脱颖而出。她努力学习,不断积累经验,只为在未来的舞台上,展现出更加精彩的自己。
冰糖的个人经历也充满了色彩。她曾经从事过美发和营销的工作,这些经历不仅锻炼了她的沟通能力与团队协作能力,也让她对时尚有了更深入的理解与感悟。她将这些经验融入到自己的表演中,展现出与众不同的魅力与气质。

冰糖,这位清纯如晨曦,灵动似春水的时尚新星,正在用自己的努力与才华,在时尚的舞台上绽放光彩。她的每一次尝试,都让我们看到了她的潜力与未来。她的每一次表演,都让我们感受到了她的魅力与热情。相信在不久的将来,冰糖会成为时尚界的一颗璀璨之星,为我们带来更多的惊喜与感动。让我们一起期待冰糖的未来,期待她在时尚的舞台上,绽放出更加耀眼的光芒!




