向日葵的花盘里面那些籽儿的排列,就像是数学家量出来的。

一圈圈的螺旋,都是算好的

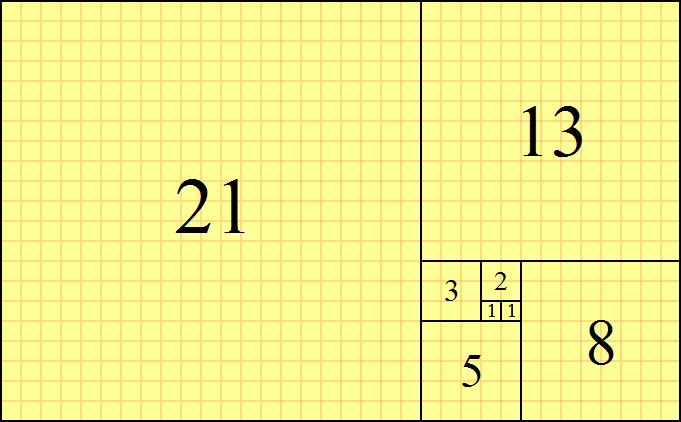
向日葵花盘上的种子,是排成两组螺旋线的,一组顺时针,一组逆时针,而且这两组螺旋线的数目,经常是斐波那契数列当中的数字。斐波那契数列就是1,1,2,3,5,8,13,21,34,55,89,144……一直排下去,后面的数总是前面两个数加起来。
比如小小的向日葵花盘,你可能会数出34条顺时针的,55条逆时针的,再大一点,可能是55和89,或者89和144,这些数呢,都是挨着的斐波那契数列里的,而且,144-89=55,89-55=34,这么减下去,还是那个数列。
除了这个,花盘正中的种子,每一颗新长出来的,与前一颗的偏转角度,不多不少,就是137.5度,这个角度叫“黄金角”,误差非常小,只有0.1度,就是这个角度,让花盘上的籽儿排得很紧,地方用得很满。
不是巧合,是植物自己长出来的,研究说,这背后是植物“生长素”在起作用,生长素在花盘分生组织里分布不均,形成了特定模式,最后就长成了螺旋。新种子形成时,会控制周围再长一个,保证间距,这个过程也遵循数学规律,还有一个“反应扩散模型”,生长素在组织里扩散反应,也遵循数学方程,导致了螺旋。
黄金角的出现,是物理化学规律下的比较稳定和省能量的模式。角度小了,花盘上就有空缺;角度大了,也一样有空缺。只有等于黄金角时,种子才能挤得最紧。

这么排有什么好处呢,一,每个籽儿都能晒到太阳,不被挡着,授粉发育也好,二,空间利用率高,有限的地方长最多的籽儿,繁殖效率高,第三,排列均匀,花盘结构稳定,养分也能均匀分配。
这种数学规律,向日葵有,松果、菠萝、雏菊这些植物的花盘或者果实上也能看到,这就表明这套玩法在植物进化中很吃香。

大自然怎么就看上了这套数学?
为什么自然选择会偏爱黄金角和斐波那契数列?其实就一句话:提高资源利用效率。把种子往有限的空间里头塞进去,还得让每个种子都能喝到水、晒到太阳。
有人研究过,如果排列不是按照黄金角来排,种子之间就会有空缺或者挤得很紧,那么空间的利用效率就低了。用计算机模拟也证明了这一点。英国数学家H·伏格尔用计算机模拟向日葵原基的生长,发现只有发散角是黄金角的时候,圆点排得密,没有空缺。

这就像植物界的“生育KPI”,哪怕只是小小的效率差别,在几千年乃至几百万年的进化尺度上,差别就变得巨大,那些能长出更接近黄金角和斐波那契数列排列的向日葵,每年多结一点种子,或者发芽率稍微高一点点,这些微小的优势一代代传递下去,最后就成了主流。
当然也不是所有植物都这样“数学强迫症”,有些植物可能通过增加花盘大小或改变形状来提升效率,策略五花八门,但向日葵的这种准确,确实是个优化选择。


人类怎么发现的?
13世纪意大利数学家斐波那契提出斐波那契数列,起初用于计算兔子繁殖问题,并未与植物建立联系
文艺复兴时期达·芬奇绘制众多植物,其对植物形态观察入微,却未明确提及数学规律
17世纪开普勒发现向日葵花盘排列与黄金比例相关,但未提供数学解释
19世纪,瑞士的勃洛克兄弟对植物的螺旋排列做了系统的探究,察觉到向日葵的螺旋线数目属于斐波那契数,不过当时并没有太放在心上。
到了20世纪初,数学家和生物学家开始合作,图灵等人提出了“反应扩散模型”,他们认为生物的形状是由化学物质相互作用,互相扩散而形成的,并不需要集中控制,这让人们有了新的思路去理解向日葵的数学规律。
到了21世纪,尤其是2013年的时候,有人用数学模型来描绘生长素和某种营养素之间的相互作用,最后预测出了生长素集中的地方和方式,这跟真的向日葵花盘一模一样,于是就证明了生长素起着关键作用。
现代技术助力深入探究向日葵生长机制

梵高画的《向日葵》系列,他对向日葵花盘的数学规律很喜欢,画里就有螺旋排列、斐波那契数列,说明人早在科学解释之前就能感知到这种数学美。

向日葵的数学机制为人类科技创新提供了很多灵感
比如太阳能板的排列,传统的太阳能板是直线排列的,会有阴影,仿照向日葵花盘的螺旋排列,采用黄金角排列,可以减少阴影,提高光能接收率,据说可以提高20%左右。
通信领域。光纤、电缆怎么在小空间塞进最多?学向日葵!用黄金角排列,最密堆积,提高空间利用率。海底光缆设计就是这么做的。
建筑设计。有些现代建筑的穹顶、采光窗格,就用了向日葵花盘的数学规律,好看,结构还稳当,材料也省。
传感器阵列的设计也是一样,无人机,自动驾驶汽车的视觉系统,如果用黄金角来排列传感器,可以提升图像质量和识别精度。
艺术与设计领域中,向日葵螺旋及黄金比例常作为创作元素
向日葵这套设计,资源利用率高,适应性强,还好看。当然把自然设计放到技术上,也存在挑战,比如怎么适应不同场景,怎么工程化,怎么平衡自然评价和工程评价标准。





